Probabilistic Model of Tandem Repeats
We model alignment of two tandem copies of a pattern of length n by
a sequence of n independent Bernoulli trials (coin-tosses). The probability
of success, P(Heads), which we also call 
or matching probability, represents the average percent identity
between the copies. Each head in the Bernoulli sequence is interpreted as a
match between aligned nucleotides. Each tail is a mismatch, insertion or deletion.
A second probability, 
or indel
probability, specifies the average percentage of insertions and deletions
between the copies. Figure 1 illustrates the underlying idea for the model.
 |
We are interested in the distribution of Bernoulli sequences and the properties
of alignments that they represent when dealing with a specific pair (,),
for example, ( = .80,
= .10). Note that these conservation parameters serves as a type of extremal
bound, i.e., as a quantitative description of the most divergent copies
we hope to detect.
The program has detection and analysis components. The detection component uses a set of statistically based criteria to find candidate tandem repeats. The analysis component attempts to produce an alignment for each candidate and if successful gathers a number of statistics about the alignment (percent identity, percent indels) and the nucleotide sequence (composition, entropy measure).
We assume that adjacent copies of any pattern will contain some matching characters
in corresponding positions. Just how many matches and how the distance between
those matches should vary depend on the fixed values of
and . We use statistical criteria
to answer these questions.
The algorithm looks for matching nucleotides separated by a common distance d, which is not specified in advance. For reasons of efficiency it looks for runs of k matches, which we call k-tuple matches. A k-tuple is a window of k consecutive characters from the nucleotide sequence. Matching k-tuples are two windows with identical contents and if aligned in the Bernoulli model would produce a run of k heads. Because we limit ourselves to k-tuple matches, we will not detect all matching characters. For example, if k=6 and two windows contain TCATGT and TCTTGT we will not know that there are 5 matching characters because the window contents are not identical. Put in terms of the Bernoulli model, the aligned windows would be represented by the sequence HHTHHH which is not a run of 6 heads.
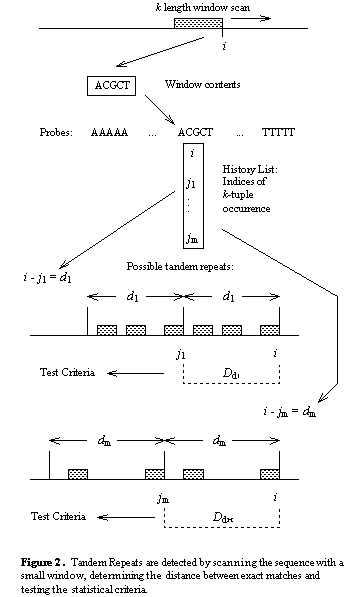
The basic operation of the detection component is illustrated in the figure
below. Let S be a nucleotide sequence. We select a small integer k,
for the tuple or window size (k=5 for example) and keep a list of all
possible k-length strings (there are 
for the DNA alphabet {A,C,G,T}) which we call the probes. By sliding the window
across the sequence, we determine the probe at each position i in S.
For each probe p, we maintain a history list 
of the positions at which p occurs.
When a position i is added to ,
we scan for all earlier occurrences
of p. Let one earlier occurrence be at j. Since i and j
are the indices of matching k-tuples, the distance d=i-j is a
possible pattern size for a tandem repeat. For the criteria tests, we
need information about other k -tuple matches at the same distance d where the
leading tuple occurs in the sequence between j and i. A distance
list 
stores this information.
It can be thought of as a sliding window of length d which keeps track
of the positions of matches and their total.
List is updated every time
a match at distance d is detected. Position i of the match is
stored on the list and the total is increased. The right end of the window is
set to i and matches that occurred before j=i-d are dropped from the
list and subtracted from the total. Lists for other nearby distances are also
updated at this time (see Random Walk Distribution ), but
only to reset their right ends to i and remove matches that have been
passed by the advancing windows. Information in the updated distance lists is
used for the sum-of-heads and apparent-size criteria
tests. If both tests are successful, the program moves on to the analysis component.
 |
The statistical criteria are based on runs of heads in Bernoulli sequences,
corresponding to matches detected with the k-tuples and stored in the
distance lists. The criteria are based on four distributions which depend upon
1) the pattern length, d, 2) the matching probability, ,
3) the indel probability, ,
and 4) the tuple size, k. For each distribution, we either calculate
it with a formula or estimate it using simulation. Then, we select a cutoff
value that serves as our criterion.
This distribution indicates how many matches are required for a specific distance
or pattern length. Let the random variable 
= the total number of heads in head runs of length k or longer in an
iid Bernoulli sequence of length d with success probability .
The distribution of is
well approximated by the normal distribution and its exact mean and variance
can be calculated in constant time. For the sum-of-heads criterion, we
use the normal distribution to determine the largest number, x, such
that 95% of the time ≥
x. For example, if
= .75, k = 5 and d = 100, then the criterion is 26. Put another
way, if a pattern has length 100 and aligned copies are expected to match in
75 positions, then by counting only matches that fill a window of length 5,
we expect to count at least 26 matches 95% of the time.
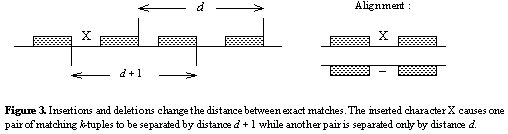
This distribution describes how distances between matches may vary due to indels.
Because indels change the distance between matching k -tuples (figure
below), there will be situations where the pattern has size d, yet the distance
between matching k-tuples is d±1, d±2, etc. In order to
test the sum-of-heads criterion, we count the matches in 
,
for Δd = 0,1,...,
for some . In our model, indels are single nucleotide events occurring with
probability . Insertions and
deletions are considered equally likely and we treat the distance change as
a problem of random walks. Let the random variable 
= the maximum displacement from the origin of a one dimensional random walk
with expected number of steps equal to 
.
It can be shown that 95% of the time the random walk ranges between ± 
.
We set = |
| . For example if = 0.1 and
d = 100, then =
7.
 |
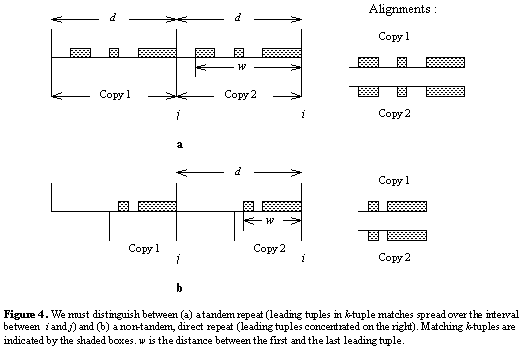
This distribution is used to distinguish between tandem repeats and non-tandem
direct repeats (figure below). For tandem repeats, the leading tuple in matching
k-tuples will be distributed throughout the interval from j to
i, whereas for non-tandem repeats, they should be concentrated on the
right side of the interval near i. Let the random variable 
= The distance between the first and last run of k heads in an iid Bernoulli
sequence of length d with success probability .
is the apparent size
of the repeat when using k-tuples to find the matches and will usually
be shorter than the pattern size d. We estimate the distribution of
by simulation because we make it conditional on first meeting the sum-of-heads
criterion. For given d,k, and ,
random Bernoulli sequences are generated using .
For every sequence that meets or exceeds the sum-of-heads criteria, the distance
between the first and last run of heads of length k or larger is recorded.
From the distribution, we determine the maximum number y such that 95%
of the time is greater
than y . We use y as our apparent size criterion. For example,
if = .75, k = 5 and
d = 100, then the criterion is 56. In order to test the apparent- size
criterion, we compute the distance between the first and last tuple on list
. If the distance between
the tuples is smaller than the criterion, we assume the repeat is not tandem
or that we have not yet seen enough of it to be convinced.
 |
This distribution is used to pick tuple sizes. Tuple size has a significant
inverse effect on the running time of the program because increasing tuple size
causes an exponential decrease in the expected number of tuple matches. If the
nucleotides occur with equal frequency, then increasing the tuple size by Δk
increases the average distance between randomly matching tuples by a factor
of 
. If k=5, the average
distance between random matches is approximately 1Kb, but if k=7, the
average distance is approximately 16Kb. Thus, by using a larger tuple size,
we keep the history lists short. On the other hand, increasing the tuple size
decreases the chance of noticing approximate copies because they may not contain
a long, unbroken run of matches. Let the random variable 
= the number of iid Bernoulli trials with success probability
until the first occurrence of a run of k successes.
follows the geometric distribution of order k. If we let p =
and q=1-p then the exact probability
for x ≥ 0 is given by the recursive formula :
 |
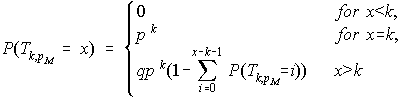For example, if = .75 and
k = 5 then we need at least 31 trials (coin-tosses) to have a 95% chance
of seeing a run of 5 heads. For patterns smaller than 31 characters, we need
to use a smaller k-tuple. The waiting time distribution allows us to
balance the running time and sensitivity of our algorithm by picking a set of
tuple sizes, each applying to a different range of pattern sizes. The
program processes the sequence once, simultaneously checking these different
tuple sizes. We require that the smallest pattern for tuple size k have
a sum-of-heads criterion of at least k+1. The table below shows the range
of tuple sizes and the corresponding pattern sizes currently used by the program.
 |
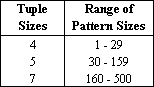If the information in the distance list passes the criteria tests, a candidate pattern consisting of positions j+1...i, is selected from the nucleotide sequence and aligned with the surrounding sequence using wraparound dynamic programming (WDP). If at least two copies of the pattern are aligned with the sequence, the tandem repeat is reported. Several implementation details of the analysis component are described below.
• Multiple Reporting of Repeat at Different Pattern Sizes :
When a single tandem repeat contains many copies, several pattern sizes are possible. For example, if the basic pattern size is 26, then the repeat may be reported at sizes 26, 52, 78, etc. We limit this redundancy in the output to, at most, three pattern sizes. Note that we do not automatically limit the output to the smallest period size because a much better alignment may come from a larger size.
• Narrow Band Alignment :
Alignments are the program's most time intensive calculations. To decrease
running time, we limit WDP calculations to a narrow diagonal band in the alignment
matrix for patterns larger than 20 characters. In accordance with the random
walk results, the band radius is .
The band is periodically recentered around a run of matches in the current best
alignment.
• Consensus Pattern and Period Size :
An initial candidate pattern P is drawn from the sequence, but this is usually not the best pattern to align with the tandem repeat. To improve the alignment, we determine a consensus pattern by majority rule from the alignment of the copies with P. The consensus is used to realign the sequence and this final alignment is reported in the output. Period size is defined as the most common matching distance between corresponding characters in the alignment and may not be identical to consensus size.
Input to the program consists of a sequence file and the following parameters ( allowable parameters values are shown in the main window ) :
1) Alignment weights for match, mismatch and indels. These parameters are for Smith-Waterman style local alignment using wraparound dynamic programming. Lower weights allow alignments with more mismatch and indels. Match weight is +2 in all options here. Mismatch and indel weights ( interpreted as negative numbers are either 3, 5, or 7. 3 is more permissive and 7 is less permissive of these types of alignments choices.
2) Matching probability and
indel probability .
= .80 and = .10 by default
and can only be modified in the console version of the program.
3) A maximum period size for patterns to report. Period size is the program's best guess at the pattern size of the tandem repeat. The program will find all repeats with period size between 1 and 2000, but the output table can be limited to some other range.
4) A minimum alignment score to report repeat. The alignment of a tandem repeat must meet or exceed the alignment score to be reported.
Tandem Repeats Finder finds repeats for period sizes in the range from 1 to 2000 nucleotides. If a repeat contains many copies, then the same repeat will be detected at various period sizes. This is restricted to the three best scoring period sizes. For example if a tandem repeat has period size 3 and contains 30 copies, then it will most likely also be detected at size 6 with 15 copies and size 9 with 7.5 copies. Also, the same period size may be detected more than once with different scores and slightly different indices.
|
Last revised October 20, 2022
Send any questions or comments to: Gary Benson |